Mounting pressure on healthcare budgets has led to an increased emphasis on economic evidence to guide healthcare policy and practice decisions. This has meant an increase in demand for information concerning the costs and effectiveness of health technologies in order to determine their cost-effectiveness. The aim of cost-effectiveness analysis is to identify efficient use of scarce healthcare resources, through identifying the treatments and technologies that provide the maximum additional effects per additional unit of resource consumed. The same principles apply to the treatments, programmes and technologies that comprise mental health services, and there is a growing literature concerning the cost-effectiveness of these various services.
The cost-effectiveness acceptability curve (CEAC) is a relatively new concept that is featuring more frequently in cost-effectiveness papers within the medical literature. These curves illustrate the uncertainty surrounding the estimate of cost- effectiveness and were developed as a result of considerable debate regarding the best way to deal with such uncertainty (Reference Van Hout, Al and GordonVan Hout et al, 1994; Reference Briggs and FennBriggs & Fenn, 1998; Reference Briggs and GrayBriggs & Gray, 1999; Reference O'Brien and BriggsO'Brien & Briggs, 2002). Since their conception, use of CEACs has become widespread within applied studies, including a number in the mental health field (Reference Bower, Byford and BarberBower et al, 2003; Reference Byford, Knapp and GreenshieldsByford et al, 2003; Reference Haddock, Barrowclough and TarrierHaddock et al, 2003; Reference Miller, Chilvers and DeweyMiller et al, 2003; Reference Scott, Palmer and PaykelScott et al, 2003; Reference McCrone, Knapp and ProudfootMcCrone et al, 2004). It has thus become important to understand what CEACs look like, how they are constructed, what they represent and how they should be interpreted. We discuss these issues with reference to recent papers (from this journal) that have included CEACs (Reference Haddock, Barrowclough and TarrierHaddock et al, 2003; Reference Scott, Palmer and PaykelScott et al, 2003; Reference McCrone, Knapp and ProudfootMcCrone et al, 2004). We focus on CEACs derived from comparisons of two interventions. For evaluations comparing more than two interventions, see Fenwick et al (Reference Fenwick, Claxton and Sculpher2001).
WHAT DOES A CEAC LOOK LIKE?
A CEAC shows the probability that an intervention is cost-effective compared with the alternative, given the observed data, for a range of maximum monetary values (l) that a decision-maker might be willing to pay for a particular unit change in outcome. A typical example of a CEAC is illustrated in Scott et al (Reference Scott, Palmer and Paykel2003: Fig. 1). Their figure shows the probability that cognitive therapy is cost-effective compared with standard clinical management with antidepressants, for a range of monetary values that a decision-maker might consider the maximum acceptable to avoid a depressive relapse. This range of maximum monetary values, expressed as £ per depressive relapse avoided, is given on the x-axis. Given a specified value of this ‘acceptable’ cost-effectiveness ratio (a point on the x-axis), the CEAC shows the probability that the data are consistent with a true cost-effectiveness ratio falling below that value (read off the y-axis).
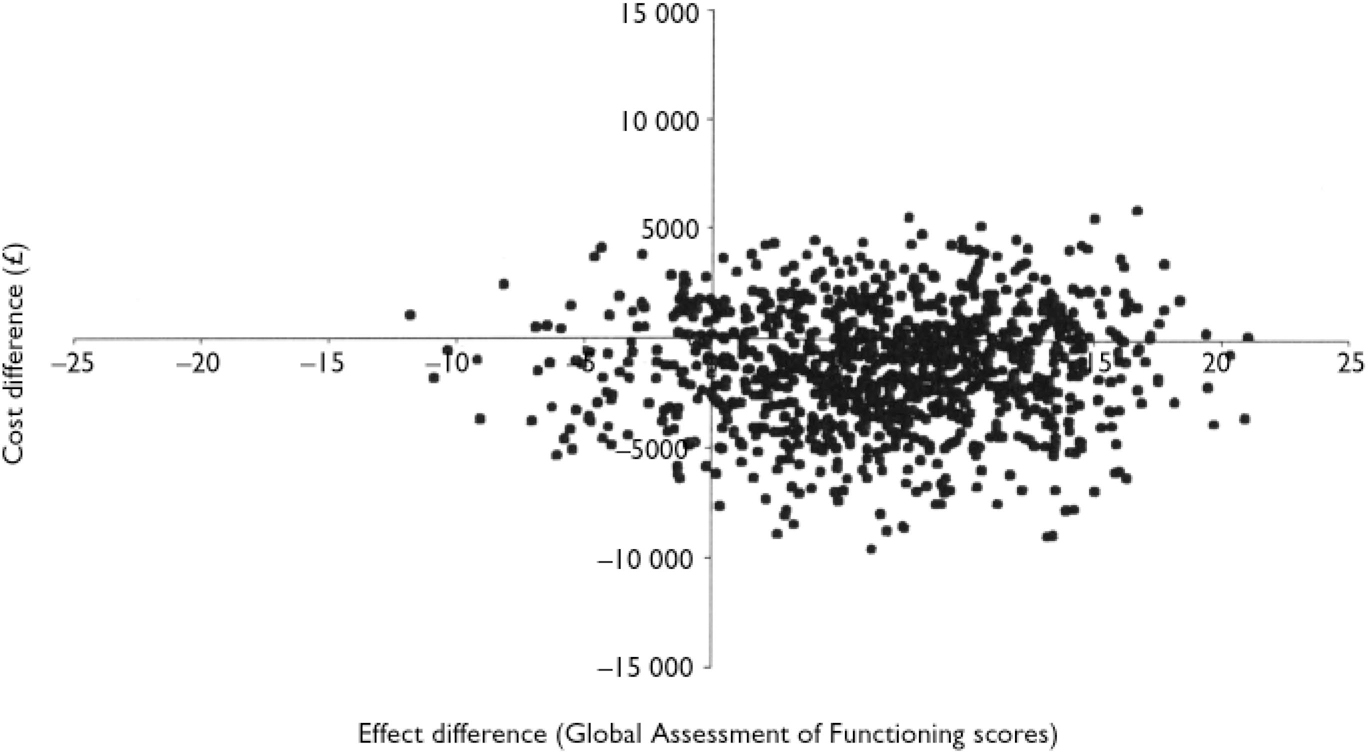
Fig. 1 Scatter plot showing the mean differences in costs and in the primary outcome measure (Global Assessment of Functioning) from the trial data using 1000 bootstrap replicates (differences based on cognitive-behavioural therapy minus control). (Taken from Reference Haddock, Barrowclough and TarrierHaddock et al, 2003.)
HOW IS A CEAC CONSTRUCTED?
Cost-effectiveness acceptability curves were introduced as an alternative to producing confidence intervals around incremental cost-effectiveness ratios (ICERs), which can be statistically challenging (Reference Van Hout, Al and GordonVan Hout et al, 1994; Reference Briggs and FennBriggs & Fenn, 1998). The CEAC is derived from the joint distribution of incremental costs and incremental effects. The most common technique for estimating these joint distributions is non-parametric bootstrapping of the observed data, although other methods are available (Reference Van Hout, Al and GordonVan Hout et al, 1994; Reference Lothgren and ZethraeusLothgren & Zethraeus, 2000; Reference O'Brien and BriggsO'Brien & Briggs, 2002). A scatter plot of the bootstrapped incremental costs and effect pairs can be presented on the incremental cost-effectiveness plane, as shown in Fig. 1 (taken from Reference Haddock, Barrowclough and TarrierHaddock et al, 2003). This illustrates the uncertainty surrounding the estimates of expected costs (here in £) and expected effects (Global Assessment of Functioning (GAF) scores) associated with the intervention (cognitive-behavioural therapy and motivational intervention) compared with the alternative (routine treatment).
The incremental cost-effectiveness plane is divided into four quadrants by the origin, with each quadrant having a different implication for economic evaluation. The SE quadrant, with negative costs and positive effects, represents the position where the intervention is more effective and less costly than the alternative (‘dominates’). Interventions falling in this quadrant are always considered cost-effective regardless of the maximum acceptable ratio (l). The NW quadrant, with positive costs and negative effects, represents the position where the intervention is both more costly and less effective than the alternative (‘dominated’). Interventions falling in this quadrant are never considered cost-effective regardless of λ. The NE quadrant, with positive costs and positive effects, and the SW quadrant, with negative costs and negative effects, involve trade-offs. These two quadrants represent the situation where the intervention may be cost-effective compared with the alternative, depending upon whether the ICER is above or below the given value of λ.
As illustrated in Fig. 1, the scatter plot commonly covers all four quadrants, indicating uncertainty about whether or not the intervention is cost-effective, and at what value it is cost-effective. The purpose of the CEAC is to summarise this uncertainty.
The CEAC is constructed by plotting the proportion of the costs and effects pairs that are cost-effective for a range of values of λ. This proportion is easily identifiable from the incremental cost-effectiveness plane as the proportion of points falling to the south and east of a ray through the origin with slope equal to λ. The process of constructing a CEAC begins by calculating this proportion with a ray of slope zero (equivalent to the x-axis). The process is repeated numerous times for rays of larger and larger slopes, up to a maximum value for l of infinity (equivalent to the y-axis).
Points in the NW quadrant are never considered cost-effective and therefore never counted. Points in the SE are always considered cost-effective and therefore always counted. As the slope of the ray is increased from zero to infinity, points in the NE and SW quadrants may or may not be considered cost-effective depending upon the value of l. For more details concerning the shape of the CEAC see Fenwick et al (Reference Fenwick, O'Brien and Briggs2004).
To illustrate this using the example from Haddock et al (Reference Haddock, Barrowclough and Tarrier2003), 693 out of 1000 bootstrap re-samples involved cost savings (fell below the x-axis), hence 69.3% of the costs and effects pairs fell to the south and east of a ray with slope zero, and as a result the CEAC crosses the y-axis at 69.3%. For a ray with a slope of £20 per point increase in GAF score, the proportion of the re-samples that were cost-effective was 70%, and for a ray with a slope of £655 per point increase in GAF score the proportion was 90%. In this way, a CEAC is generated.
HOW IS A CEAC INTERPRETED?
The CEAC indicates the probability that the intervention is cost-effective compared with the alternative, given the data and for a given value of the maximum acceptable ratio (l). In the example of Haddock et al (Reference Haddock, Barrowclough and Tarrier2003), given a maximum acceptable ratio of £20 per point increase in GAF score, the probability that cognitive-behavioural therapy is cost-effective compared with routine treatment is 0.7. This is equivalent to stating that, given the data, there is a 70% chance that the additional cost of cognitive-behavioural therapy, compared with routine treatment, is less than £20 per point increase in GAF score. Note the comparative nature of both statements. It is not equivalent to stating that cognitive-behavioural therapy has a 70% chance of costing less than £20 per point increase in GAF score.
Care must be taken when interpreting the information provided by a CEAC. A CEAC simply presents the probability that an intervention is cost-effective compared with the alternative for a range of values of λ. That is, the probability that the ICER falls below the maximum acceptable ratio. Statements concerning CEACs should be restricted to the uncertainty of the estimate of cost-effectiveness. The information from a CEAC should not, in general, be used to make statements about the implementation of the intervention.






eLetters
No eLetters have been published for this article.