Psychopathy is the key construct in the Dangerous and Severe Personality Disorder (DSPD) Programme, yet considerable debate surrounds the core features of this construct (e.g., Reference Chen and ThissenCooke, et al, 2004; Reference Rogers and SchmittSkeem et al, 2003; Reference Forouzan and CookeHare &Neumann, 2005). Within DSPD assessment, a measure of psychopathy, the Psychopathy Checklist – Revised (PCL–R; Footnote 1 Reference Floyd and WidamanHare, 2003), is central for selection. A fundamental criticism of the PCL–R as a measure of psychopathy is that it confounds two distinct constructs – personality disorder and criminal behaviour (Reference Hill, Neumann and RogersLilienfeld, 1994). Failure to disaggregate the measurement of these two constructs renders it impossible to argue persuasively that psychopathic personality disorder produces criminal behaviour (Reference Andershed, Kerr and StattinBlackburn, 1988; Reference Chen and ThissenCooke et al, 2004). The demonstration of such a link is necessary to detain an individual under Article 5 of the European Convention on Human Rights. Definitions of psychopathy that entail criminal behaviour have long been recognised as essentially tautological (Reference Cooke, Michie and HartEllard, 1988). In this paper we argue that measures and constructs of psychopathy are confused and that the introduction of inappropriate statistical methods has led to criminal behaviour being placed at the centre of the definition of the disorder. The tautology is thereby perpetuated.
MEASURES AND CONSTRUCTS
There are significant dangers when measures and constructs are confused;this is particularly the case under operationalism, where the measure is conflated with the construct (Reference BandalosCampbell, 1960). Scores on the PCL–R are now being confused with the construct of psychopathy (see Reference OdgersSkeem &Cooke, 2007). This forecloses on the possibility of examining the mapping of the theoretical construct (psychopathy) onto the empirical observation (PCL–R scores). Factor analysis is a tool that can inform our understanding, given its explicit recognition that all measures are fallible indicators of constructs; manifest variables (measures) are the product both of latent variables (constructs) and error. Hence, factor analytical approaches assume that latent variables produce the thoughts, feelings and modes of behaviour that are measured or recorded by item scores plus error (Reference Cooke, Michie and HartEdwards &Bagozzi, 2000). Factor analysis can partition the variance associated with each item into two parts: common variance, or variance associated with latent variables, and unique variance, or variance specific to that item and random error. Factor analysis thus explicates the multivariate relationships among the latent variables (constructs) that together influence the item ratings (empirical observations).
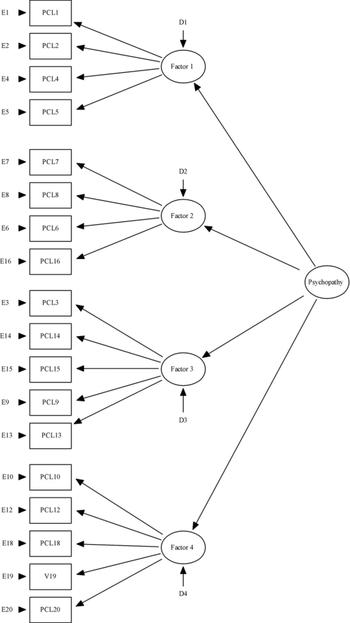
The structure of the PCL–R and its antecedents has been the subject of some debate. The original PCL–R manual (Reference Edwards and BagozziHare, 1991) lacked clarity about the structure of the test (Reference ByrneCooke& Michie, 2001). For a number of years a two-factor model dominated the literature (Reference Gottfredson and HirschiHarpur et al, 1988). Unfortunately, the support for this model was over-reliant on congruence coefficients; these provide inadequate tests of the similarity of factor solutions across samples. Cooke & Michie (Reference Byrne2001), using item response theory, confirmatory factor analysis and cluster analytical methods, argued that 13 of the 20 PCL–R items are conceptually distinct and psychometrically non-redundant indicators of psychopathy. Since they were found to be relatively poor indicators of psychopathy, items that tapped antisocial behaviour largely were excluded. Cooke & Michie (Reference Byrne2001) developed a well-fitting hierarchical structure in which the superordinate trait, psychopathy, overarched three highly correlated symptom factors: arrogant and deceitful interpersonal style, deficient affective experience and impulsive and irresponsible behavioural style (see Fig. 1). The first factor was specified by glibness/superficial charm, grandiose sense of self-worth, pathological lying, and conning/manipulative, the second factor by lack of remorse or guilt, shallow affect, callous/lack of empathy and failure to accept responsibility for own actions, and the third factor by need for stimulation/proneness to boredom, irresponsibility, impulsivity, parasitic lifestyle and lack of realistic, long-term goals. This model, despite being described by some as ‘controversial’ (Reference Michie and CookeSalekin et al, 2006), is conceptually coherent (Reference OdgersSkeem & Cooke, 2007) and consistent with clinical tradition (Reference ByrneCooke& Michie, 2001). Moreover, it has been replicated in a number of independent samples and by independent researchers using both the PCL (Reference HareJackson et al, 2002; Reference Rogers and SchmittSkeem et al, 2003) and other measures of psychopathic traits (Andershed et al, 2002). The three-factor model also has been shown to relate to external correlates in a theoretically coherent manner (Reference Dolan and AndersonHall et al, 2004).
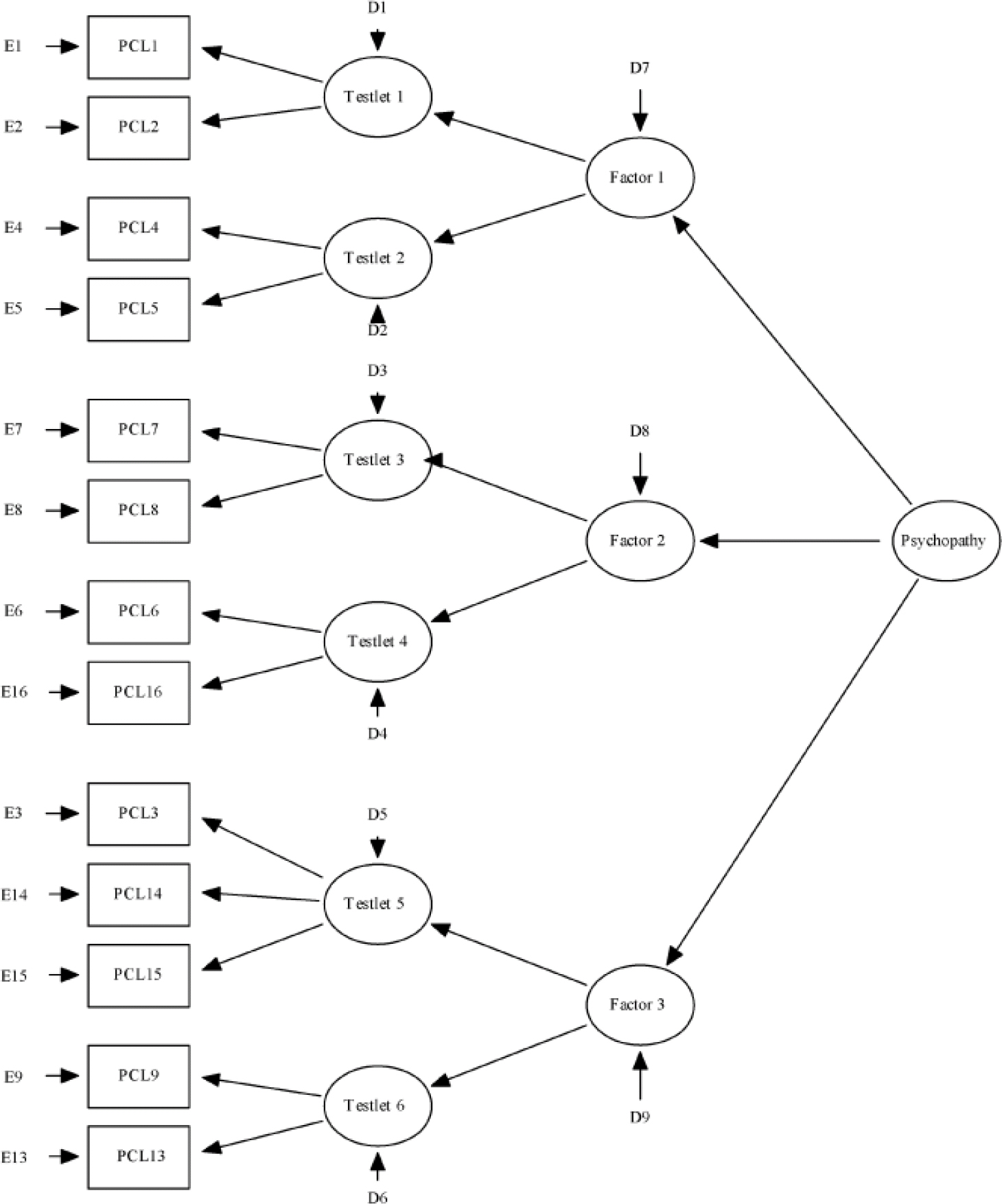
Fig. 1 Structure of the Psychopathy Checklist - Revised. Hierarchical three-factor model with testlets. PCL, Psychopathy Checklist - Revised.
There can be little doubt that the three-factor model has stimulated a number of researchers to reconsider the structure of the PCL–R measure and its implications for our understanding of the construct of psychopathic personality disorder. This must be regarded as positive: the definition and validity of constructs must be revisited as knowledge advances (Reference Rutherford, Alterman, Cacciola and GaconoSmith et al, 2003).
CRIMINAL BEHAVIOUR IN THE DIAGNOSIS OF PSYCHOPATHIC PERSONALITY DISORDER
Hare (Reference Floyd and Widaman2003) and his colleagues (Reference Forouzan and CookeHare & Neumann, 2005; Reference Little, Cunningham and ShalarNeumann et al, 2007) have argued against the three-factor model and proposed a number of four-factor models. Essentially, within these models the three factors of Cooke & Michie (Reference Byrne2001) are supplemented with a fourth ‘factor’ comprising five items related to criminal behaviour, i.e. poor behavioural controls, early behavior problems, juvenile delinquency, revocation of conditional release and criminal versatility. Previously, Hare and his colleagues had argued that psychopathy and criminality are distinct but related constructs (Reference Hall, Benning and PatrickHart et al, 1995;emphasis in original) and that psychopathy should not be confused with antisocial and criminal behaviour (Reference EllardHare, 1999).
More recently, Hare & Neumann (Reference Forouzan and Cooke2005) have argued that PCL–R items that capture antisocial tendencies, including criminality, are indicators of important psychopathic traits, asserting that the ‘real core of psychopathy has yet to be uncovered’ (p. 62). They observe that the exclusion of antisocial behaviour in the three-factor model decreases the utility of the PCL–R for predicting violence and aggression (see Reference Rogers and SchmittSkeem et al, 2003). Furthermore, they assert that ‘current findings suggest that the four-factor model has incremental validity over the three-factor in predicting important external correlates of psychopathy’ (Reference Little, Cunningham and ShalarNeumann et al, 2007: p. 22). This logic is confused. Adding variables, for example, gender, age or a history of substance misuse, would also improve prediction. However, such an improvement would not imply that these characteristics are core to psychopathic personality disorder. A measure's validity in representing the construct of psychopathy should not be confused with its utility in predicting deviant behaviour (Reference Rogers and SchmittSkeem et al, 2003).
We have argued elsewhere that there are good reasons to reject the contention that criminal behaviour should play a central role in diagnosing psychopathy; instead, such behaviour is best viewed as a secondary feature, or sequela, of the disorder (Cooke et al, Reference Chen and Thissen2004, Reference Cooke and Michie2006). In a companion paper (Reference OdgersSkeem & Cooke, 2007), we present conceptual (logical, theoretical) directions for resolving the debate about whether antisocial behaviour is an essential component or ‘downstream correlate’ of psychopathy. In the current paper, we focus on empirical (analytical) directions, demonstrating how the application of appropriate statistical methods is necessary to help advance understanding of psychopathy.
To inform the debate, we consider the appropriateness of various analytical strategies and demonstrate their impact on the model selected to describe the PCL–R. In the interests of transparency, we append as data supplements to the online version of this paper the code for all models tested (data supplement 1) together with the correlation matrix for the dataset we used (data supplement 2). This will allow other researchers to replicate – or reject – our conclusions. Our goal is to address three of the difficulties that confront the field in this debate about the structure of psychopathy. First, never are the competing models compared directly using the same dataset and the same approach to modelling. Second, the verbal descriptions of the models considered are often imprecise and thus it is hard for independent researchers to parameterise these models accurately. Third, contentious analytical approaches such as parcelling are adopted. We begin by describing the competing models, then consider key issues of method and conclude by presenting analyses to illustrate these issues of method.
THE COMPETING PPCL CL-R MODELS Footnote 2
The two-factor model
The two-factor model proposed by Harpur et al (Reference Gottfredson and Hirschi1988) suggests that the interpersonal and affective items of the PCL–R coalesce to form a factor described as ‘the selfish and remorseless use of others’ (Reference Edwards and BagozziHare, 1991, p. 76) and the items relating to behavioural instability, lack of planfulness and criminal behaviour coalesce to form a factor described as ‘the chronically unstable and antisocial lifestyle; social deviance’ (Reference Edwards and BagozziHare, 1991: p. 76). The use of modern techniques of confirmatory factor analysis has demonstrated that this model is untenable (Reference ByrneCooke &Michie, 2001; Cooke et al, Reference Cleckley2005a , Reference Cooke and Michie b ). Hare (Reference Floyd and Widaman2003) amended the two factors by adding an extra item, criminal versatility to the second factor (in the original two-factor model, this was one of three items included in PCL–R total scores, but omitted from factor scores). Below we refer to the original and amended 2-factor models.
The three-factor model
The three-factor model is illustrated in Fig. 1. There are perhaps four points of emphasis regarding this three-factor model. First, the structure is hierarchical, with a superordinate construct ‘psychopathy’ that is sufficiently unidimensional to be regarded as a coherent psychopathological construct or syndrome (Reference ByrneCooke & Michie, 2001; Cooke et al, Reference Cleckley2005a , Reference Cooke and Michie b ). This hierarchical structure reflects a common model of personality and personality disorder in which traits of different levels of generality, from general to more specific, are structured in a hierarchical manner (Reference KlineMcCrae & Costa, 1995). Second, the three factors can be regarded as having reliable general variance as a consequence of the influence of the broad psychopathy construct shared with the other factors. In addition, however, there is reliable specific variance unique to each particular factor. The value of refining the broad construct into specific factors has advantages in that the specificity between aspects of the disorder and external variables may be clearer (Reference MartensRaine et al, 2000; Reference Salekin, Brannen and ZalotSoderstrom et al, 2002; Reference Cooke and MichieDolan & Anderson, 2003; Reference Dolan and AndersonHall et al, 2004). Thus, this hierarchical model highlights ‘differential relations between the psychopathy factors and a variety of important criteria’ (Reference Little, Cunningham and ShalarNeumann et al, 2007: p. 24), but requires that the factors investigated are actually components of the general disorder of psychopathy.
Third, although some variants of the original three-factor model exclude testlets for the sake of parsimony (Reference Rogers and SchmittSkeem et al, 2003; Reference Marshall and CookeOdgers, 2005; see Fig. 2), below the level of specific factors, and between the items, are testlets. Testlets occur when items are more highly associated than can explained by their relationship with the underlying latent trait; thus, a pair of items that form a testlet can be construed as being somewhere between one and two items (Reference Bandalos, Finney, Marcoulides and SchumackerChen & Thissen, 1997). Indeed, the use of item response theory demonstrated that all PCL–R items other than poor behavioural controls form testlets (Reference ByrneCooke & Michie, 2001). Testlets do not merely capture shared error variance, instead testlets are conceptually meaningful. Testlets combine specific indicators to form higher-order facets within the hierarchy of personality features.
Fourth, the model entails only 13 of the 20 PCL–R items. The 7 excluded items primarily reflect antisocial behaviour rather than core traits;it is possible to achieve maximum scores on some of these items without any evidence that the behaviour is trait-like, i.e. persistent and pervasive. These items failed to coalesce into a coherent syndrome and form a clear structure with the three factors, and generally demonstrated poor discrimination (Cooke & Michie, Reference Blackburn1997, Reference Byrne2001).
The four-factor models
The current debate is frequently described as a choice between a three- and a four-factor model. This is misleading as there are two three-factor models and many four-factor models (Reference Floyd and WidamanHare, 2003; Reference Forouzan and CookeHare & Neumann, 2005). Frequently, authors fail to distinguish between these models and this creates conceptual confusion. We can identify at least ten four-factor – or equivalent – models in the literature. We describe these as: (a) a four-factor hierarchical model; (b) a two-factor, four-facet hierarchical model; Footnote 3 (c) a four-factor correlated model. Since each of these models can be ‘parcelled’, we also describe a four-factor parcelled model.
A four-factor hierarchical model
Hare (Reference Floyd and Widaman2003) implied that four factors (i.e. the three factors from the Cooke & Michie (Reference Byrne2001) model together with a criminality ‘factor’ specified by five items that tap criminal behaviours) are in a hierarchical relationship with the superordinate psychopathy factor (Fig. 3). Although Hare (Reference Floyd and Widaman2003) argued that the model ‘envelopes’ the three-factor model, to date no results have been provided to support this position.
A two-factor, four-facet hierarchical model
Hare (Reference Floyd and Widaman2003) asserted that ‘a superior test structure’ (p. 85) is one in which two superordinate factors (i.e. minimal modifications of the original two factors) are interposed between the four factors and the superordinate psychopathy construct (Fig. 4). Although Hare (Reference Floyd and Widaman2003) asserts that this is an improvement over ‘a model that goes directly from factors to the overall superordinate factor’ (p. 85), no results are provided to support this contention. Support is particularly important because the model specified by Hare (Reference Floyd and Widaman2003: Fig. 7.1) has several equivalents (models that yield the same covariances or correlations but have different paths among the latent variables). Indeed, the two-factor, four-facet hierarchical model has six equivalent models. For example, a correlation between factor 3 and factor 4 – or indeed, any other pair of factors – is mathematically equivalent to the one that Hare (Reference Floyd and Widaman2003) selected. When a model has mathematically equivalent versions, the models cannot be distinguished statistically. No model can be shown to be statistically superior. Instead, model selection must be based on sound theory: it is an established principle that researchers must justify their preference for a particular model over mathematically identical ones (Reference Hart, Cox and HareKline, 1998; Reference KarpmanMartens, 2005).
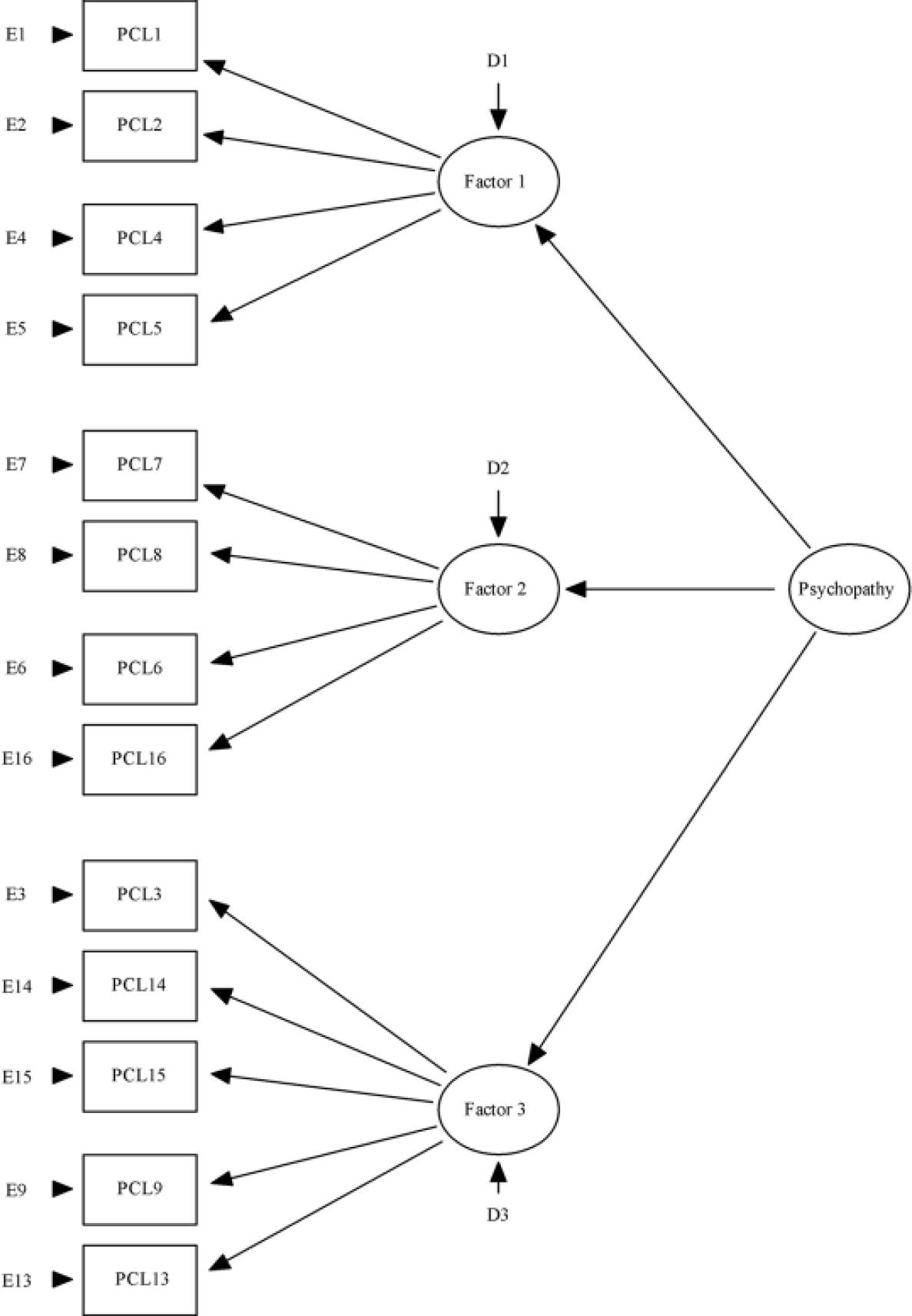
Fig. 2 Structure of the Psychopathy Checklist Revised. Degraded three-factor model (without testlets). PCL, Psychopathy Checklist - Revised.
A four-factor correlated model
A number of researchers (e.g., Reference Floyd and WidamanHare, 2003; Reference HareHill et al, 2004; Reference Forouzan and CookeHare & Neumann, 2005) have presented correlated factor models in which the three factors from the three-factor model, together with the fourth criminality ‘factor’, are all inter-correlated (Fig. 5). Hence, each factor (e.g. factor 1) is correlated with all of the other factors (e.g. factors 2, 3 and 4). Neumann et al (Reference Little, Cunningham and Shalar2007) contend that correlated factor models are superior to the hierarchical models previously offered.
Parcelled variant of the four-factor correlated model
All of these four factor models can be subjected to parcelling, a procedure where items are summed to form composites prior to factor analysis (Reference Floyd and WidamanHare, 2003). Parcelling creates even more conceptually and mathematically distinct models. Although these are described as four-factor or four-facet models, parcelling essentially yields one-factor models (i.e. one latent factor specified by four manifest composites). For illustrative purposes, we present the parcelled two-factor four-facet hierarchical model (Fig. 6).
ISSUES OF METHOD IN TESTING MODEL FIT
The debate raises methodological issues about how best to model the structure of a test such as the PCL–R.
Correlated v. hierarchical models
The work of Hill et al (Reference Hare2004) highlights the emerging difficulty in distinguishing between hierarchical and non-hierarchical models (Reference Forouzan and CookeHare & Neumann, 2005; Reference Little, Cunningham and ShalarNeumann et al, 2007). A key feature of a hierarchical model is the demonstration that the higher order construct of interest is sufficiently unidimensional to be regarded as a coherent psychopathological syndrome. For two- or three-factor models, all correlated models are inherently hierarchical in that they are mathematically equivalent to models with a superordinate factor overarching subordinate factors. For models with four or more factors, this is no longer the case. In terms of statistical modelling, a PCL–R three-factor correlated model has three correlations among the factors, and the hierarchical model also has three loadings on the superordinate psychopathy factor. In contrast, the PCL–R four-factor correlated model has six correlations among the factors, whereas the hierarchical model has four loadings on the superordinate psychopathy factor. The hierarchical model is more parsimonious, more constraints being placed on the model, and thus it is a more demanding model to fit.
Nevertheless, proponents of the four-factor model strongly favour nonhierarchical models: ‘we recommend using first-order models with correlated factors in future research’ (Reference Little, Cunningham and ShalarNeumann et al, 2007). The assumption is that ‘the strong correlations between the factors… reveal that they are indicators for a second-order latent variable’ (Reference Little, Cunningham and ShalarNeumann et al, 2007). This assumption that correlated and hierarchical models are the same is misleading. It is necessary to explicitly compare a four-factor hierarchical model with a four-factor correlated model.
This issue has fundamental conceptual importance. The three-factor hierarchical model implies that psychopathic personality disorder (the superordinate factor) is underpinned by distinct constellations of interpersonal, affective and lifestyle traits (the first-order factors): the expression of these trait constellations is caused both by the overarching disorder and specific variance associated with the factor. The four-factor correlated model does not imply the presence of an overarching disorder that produces particular symptoms. Instead, these symptoms could be merely a hodge-podge of domains that co-occur. Essentially, the correlated model implies a compound trait composed of distinct constructs without a common cause (Reference Rutherford, Alterman, Cacciola and GaconoSmith et al, 2003). For example, measures of psychopathy are often associated with indices of alcohol and drug misuse and/or addiction (Reference McCrae and CostaRutherford et al, 2000). Most authorities, however, would not construe substance misuse and addiction as central to psychopathy, but rather view them as associated features of the disorder (Reference Bentler and WuCleckley, 1988; Reference Skeem and MulveyWorld Health Organization, 1992; American Psychiatric Association, 1994). This can be tested empirically by comparing the relative fit of a hierarchical v. a correlated model, each with four factors: the interpersonal, lifestyle and affective factors of the PCL–R and a fourth ‘addiction’ factor. If the authorities are right about the lack of centrality of addiction to psychopathy, the hierarchical model will not fit whereas the correlated factor model will.
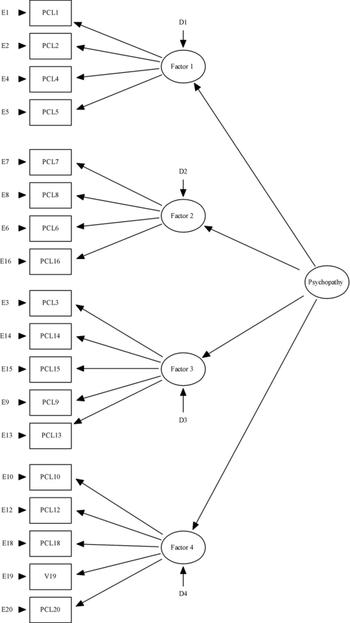
Fig. 3 Structure of the Psychopathy Checklist Revised. Hierarchical four-factor model. PCL, Psychopathy Checklist - Revised.
This is equally true for the inclusion of items that essentially are counts of antisocial behaviours in the model. If a hierarchical model fits, one could argue that antisocial behaviours are a core part of the disorder. If the correlated model fits, one can only assume that antisocial behaviours are correlated with psychopathy; perhaps a self-evident, if not trivial, observation. The distinction between correlated and hierarchical models is thus core to this debate.
There are no reasonable arguments for neglecting this distinction. Proponents of the four-factor model argue that if the four factors have differential associations with external correlates, then it would be unwise to employ a superordinate model to seek out such differential associations. This argument conflates the scoring and application of a measure (PCL–R total scores or PCL–R factor scores) with the understanding of a construct (psychopathy, with specific trait constellations). Hierarchical models represent specific factors that underpin superordinate constructs. Unlike correlated models, hierarchical models require that the specific factors included in the model be part of a coherent construct. Thus, hierarchical models have great potential for understanding both psychopathic personality disorder and its specific components.
The use of testlets v. correlated errors
Local dependency occurs when there is consistency among item responses that cannot be explained by individual differences on the latent trait being measured. Testlets are groups of items that show local dependence (a testlet formed of two items may be viewed as somewhere between one and two items). Although local dependence can emerge for a variety of reasons, with a rating scale the most common reason is the overlap of item definitions. PCL–R definitions are often overlapping. For example, ‘lack of remorse or guilt’ and ‘failure to accept responsibility for own actions’ both require consideration of whether the individual externalises blame. In creating the screening version of the PCL–R (the PCL–SV), Hare and colleagues recognised this issue and grouped conceptually related PCL–R items to produce distinct PCL–SV items (Reference Hall, Benning and PatrickHart et al, 1995; Reference CampbellCooke et al, 1998).
If there is consistent evidence that testlets exist within a scale this indicates local dependence. Local dependence is an undesirable property of a scale for three reasons. First, local dependence complicates the structure underpinning the data and can incorrectly challenge the assumption that a unidimensional trait underpins the test. This is crucial if data are to be subjected to parcelling. Second, local dependence leads to an overestimation of the true amount of information provided by the test. That is, the test appears to be more accurate than it actually is because information is double-counted. Third, the ratings do not allow clinicians to adequately distinguish between conceptually distinct symptoms. Although testlets can be confused with correlated errors, the two concepts are conceptually and mathematically distinct. Conceptually, unlike correlated errors, testlets explicitly describe the measurement model, specifying theoretically meaningful sub-facets within the hierarchical description of the disorder. For example, ‘x=pathological lying’ and ‘conning/manipulative’ combine to describe a deceptive interpersonal style. This was implicitly acknowledged when these two PCL–R items were combined to create the one PCL–SV item called ‘deceitful’ (Reference Hall, Benning and PatrickHart et al, 1995). Correlated errors are more opaque – they do not provide this additional level of description. Mathematically, testlets are more elegant than correlated errors. A model with a three-item testlet is more parsimonious that a model with three items with correlated errors that load on the same factor: the former requires two parameters, the latter three parameters. We are criticised for including testlets in our three-factor model (Reference Little, Cunningham and ShalarNeumann et al, 2007). In our view, any attempt to provide an accurate model of the structure of the PCL–R should consider testlets, even if only to reject the need for their inclusion in any model.

Fig. 4 Structure of the Psychopathy Checklist Revised. Hierarchical two-factor, four-facet model. PCL, Psychopathy Checklist - Revised.
The use of parcelling
In structural equation modelling a parcel is an aggregate-level indicator derived by combining individual items (e.g. adding individual PCL–R items to derive a new manifest variable; Reference Jackson, Rogers and NeumannLittle et al, 2002). This is a controversial technique (Bandalos, 2002; Reference Jackson, Rogers and NeumannLittle et al, 2002). Proponents of the technique argue that parcelling has two broad advantages. First, combining items results in composite variables with better psychometric properties than item variables (e.g. greater reliability, a higher ratio of common-to-unique factor variance, smaller and more equal intervals between scale points and distributions that are less likely to violate distributional assumptions; Reference Jackson, Rogers and NeumannLittle et al, 2002; Reference Harpur, Hakstian and HareKim & Hagtvet, 2003). Second, parcelling results in models with better fit indices. This is because they reduce sources of sampling error, require fewer parameters and are less likely to be affected by correlated residuals or dual loadings. Broadly, the number of variances and covariances that the model must account for is reduced (Bandalos, 2002; Reference Jackson, Rogers and NeumannLittle et al, 2002; Reference Harpur, Hakstian and HareKim & Hagtvet, 2003; Reference KarpmanMartens, 2005).

Fig. 5 Structure of the Pscyhopathy Checklist Revised. Correlated four-factor model. PCL, Psychopathy Checklist - Revised.
Opponents of parcelling point out five problems. First, parcelling can obscure the multidimensional nature of the items. Bandalos (2002) noted that when the assumption of unidimensionality is not met (an assumption that is rarely tested) ‘the use of parcels can obscure rather than clarify the factor structure of the data’ (p. 80). This is clearly a problem when there is evidence of local dependency, as there is with the PCL–R items (Reference ByrneCooke & Michie, 2001). Second, the improvement in fit is more apparent than real; models that do not fit at an item level can be made to appear to fit with parcelling. Bandalos & Finney (2001) noted that parcelling improves model fit, irrespective of whether the model is specified correctly or not; this also reduces our ability to detect mis-specified models. Kim & Hagtvet (Reference Harpur, Hakstian and Hare2003) demonstrated empirically that when parcelled and item models were compared, the parcelled models yielded better fit statistics. Unlike the item models, the parcelled models pointed to the acceptance of mis-specified models. Third, Bandalos (2002) reported that parcelling can bias estimates of structural parameters (e.g. path coefficients; ‘factor loadings’). Fourth, comparisons of factor structure across groups for parcelled variables vary considerably from those based on individual items (Bagozzi & Edwards, 1998). This will affect our understanding of important issues, including cross-cultural variation in psychopathy and variation across gender, age and race. Fifth, even if the use of parcelling is defensible statistically, from a clinical perspective it can result in the loss of important information about the condition being considered (Reference Jackson, Rogers and NeumannLittle et al, 2002). When one sums across several items and then examines the relation between that sum (e.g. parcelled interpersonal facet) and an external variable (e.g. dominant behaviour), it is impossible to know that one aspect of the sum (e.g. grandiosity/charm) strongly predicts the external variable, whereas the other (e.g. deception) is unrelated. Data aggregation results in a loss of information.
When is it legitimate to use parcelling to analyse PCL–R data? Justification of the approach depends on (a) the purpose of the analysis and (b) the analytical strategy adopted before parcelling is undertaken. Little et al (Reference Jackson, Rogers and Neumann2002) noted that ‘careful delineation of the goals of the study is clearly the paramount issue’ (p. 6). If the purpose of the analysis is to explicate the interrelations among items on a test for construct validation purposes, then parcelling is inappropriate (Reference Maccallum and AustinRogers &Schmitt, 2004). However, if the goal is to examine the interrelations among well-established measures of latent traits then parcelling may be appropriate. In the latter case it is assumed that the structure of the latent traits is well established (i.e. is not the subject of debate) and the primary interest is in putative causal relations among the latent traits rather than the measurement model (Reference Jackson, Rogers and NeumannLittle et al, 2002; Reference Maccallum and AustinRogers & Schmitt, 2004; Reference KarpmanMartens, 2005). Rogers &Schmitt (Reference Maccallum and Austin2004) warned, however, that even when a measure has been validated at the item level in terms of a measurement model, parcelling of these items can still result in ‘undesirable or unpredictable effects on estimates and fit when testing the theoretical model’ (p.380).
If parcelling is to be attempted, an essential prerequisite is an analysis of the dimensionality of the parcel (Bandalos & Finney, 2001; Bandalos, 2002; Reference Jackson, Rogers and NeumannLittle et al, 2002; Reference Maccallum and AustinRogers & Schmitt, 2004). Unfortunately, this is more honoured in the breach than the observance. Kim& Hagtvet (Reference Harpur, Hakstian and Hare2003) demonstrated that the unidimensionality of a parcel must be established before it is entered into a more complex model. In the absence of unidimensionality the structural relations among latent traits cannot be interpreted (Reference Jackson, Rogers and NeumannLittle et al, 2002). Kim & Hagtvet (Reference Harpur, Hakstian and Hare2003) propose a method that explicitly models the single item and parcel indicators simultaneously, allowing a comprehensive evaluation of the unidimensionality of the parcel. Interestingly, this approach is formally equivalent to the testlet approach adopted by Cooke & Michie (Reference Byrne2001). The three-factor approach with testlets provides greater understanding of the PCL–R items than a four-factor parcelled approach.
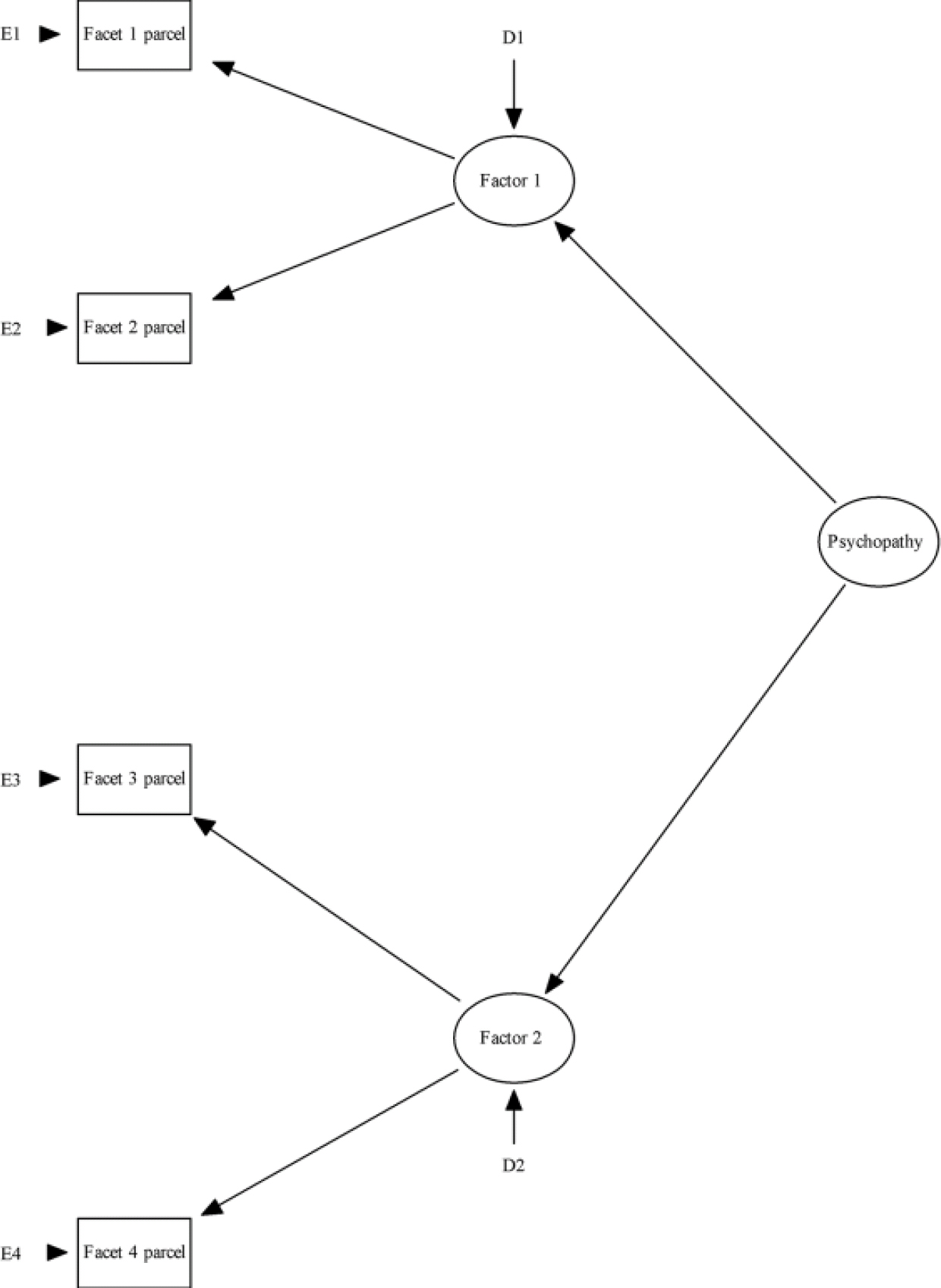
Fig. 6 Structure of the Psychopathy Checklist Revised. Two-factors, four-facet parcelled model. PCL, Psychopathy Checklist - Revised.
In summary, our understanding of the structure of the PCL–R, and to some degree our understanding of psychopathy, may be adversely influenced by the application of inappropriate methods for specifying the basic framework of the measurement model (correlated rather than hierarchical factors) and specific components (parcels rather than items and/or testlets).
DEMONSTRATION OF METHOD ISSUES
We now report a series of analyses of PCL–R data on a large sample of male offenders to illustrate the impact of using correlated v. hierarchical models, of parcelling variables prior to model fitting and of modelling local dependency with testlets. Overall these analyses demonstrate that appropriate methods are necessary for appropriate conclusions.
Participants
The sample comprised a total of 1212 adult male offenders. Footnote 4 The largest subsample comprised 608 adult male offenders from seven prisons in Her Majesty's Prison Service (HMPS) in England and Wales, selected to be representative of the HMPS population. Additional subsamples included a representative sample of 246 offenders from the Scottish Prison Service (Reference Blackburn and StrackCooke & Michie, 1999), a stratified random sample of 253 offenders from Scotland's largest prison (Reference LilienfeldMichie & Cooke, 2006) and a sample of 105 incarcerated Scottish offenders who volunteered to participate in a study of early childhood experiences (Reference Jones, Cauffman and MillerMarshall & Cooke, 1998). Only complete cases were used (n=827) to ensure that the same data were used irrespective of the model being tested.
The procedure
The PCL–R ratings were made according to instructions in the test manual (Reference Edwards and BagozziHare, 1991). All PCL–R evaluations were conducted by trained raters.
Confirmatory factor analysis
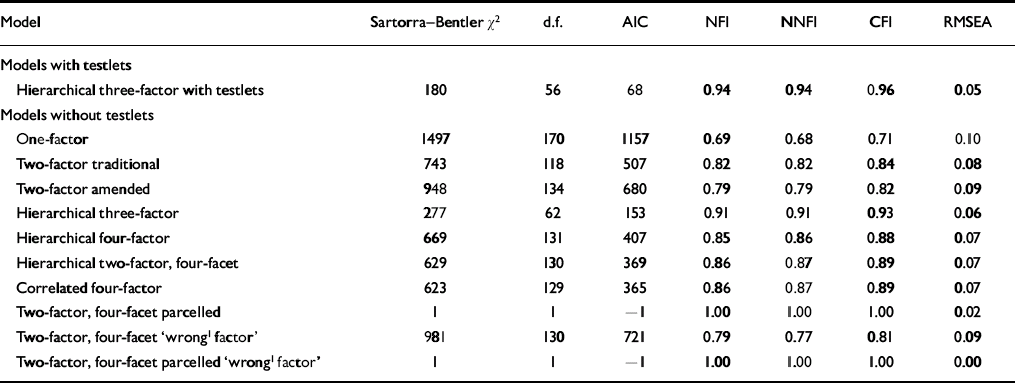
Confirmatory factor analysis permits quantification of a particular factor structure's fit within a particular sample. We assessed quality of fit using multiple indices, as each index has limitations (Reference Hart, Cox and HareKline, 1998; Reference Kim and HagtvetMacCallum & Austin, 2000). Different aspects of fit were evaluated, including absolute fit (χ2), fit adjusted for model parsimony (non-normed fit index, NNFI) and fit relative to a null model (comparative fit index, CFI), and root mean square error of approximation (RMSEA). Following convention, the criterion for adequate fit was defined as CFI and NNFI ⩾0.90 and RMSEA ⩽0.08 (Reference Bagozzi and EdwardsByrne, 1994). Following Kim& Hagvtet (Reference Harpur, Hakstian and Hare2003) we classified RMSEA values into four categories: close fit (0.00–0.05), fair fit (0.06–0.08), mediocre fit (0.08–0.10), and poor fit (>0.10).
Confirmatory factor analysis was performed using EQS for Windows (Bentler & Wu, 1995). Participants with missing data were deleted listwise for these analyses. Maximum likelihood estimation with robust-fit statistics and standard errors was used. The correlations were polychorics. Recommendations in the electronic help manual for the EQS 6 software suggested that this estimation approach is the best EQS approach for data of this type. This differs from the approach used in Cooke & Michie (Reference Byrne2001). Footnote 5 We also ran the analyses using the MPlus program with robust-weighted least-squares estimation and the same pattern of results was obtained. Footnote 6
Comparison of models
We started our analysis by estimating a one-factor model with all 20 items loading on a single latent trait. Fit statistics (Table 1) indicate that this is not a plausible model. We then tested the traditional two-factor model, which contains 8 items that load on the factor described as ‘the selfish, callous and remorseless use of others’ and 9 items that load on a factor termed ‘the chronically unstable and antisocial lifestyle; social deviance’ factor (Reference Gottfredson and HirschiHarpur et al, 1988). Fit statistics (Table 1) indicate that this too is not a plausible model. We then tested the amended two-factor model (Reference Floyd and WidamanHare, 2003), i.e. we added the item ‘criminal versatility’ to the second factor. Fit statistics (Table 1) again indicate that this is not a plausible model.
Table 1 EQS categorical variables
| Model | Sartorra–Bentler χ2 | d.f. | AIC | NFI | NNFI | CFI | RMSEA |
|---|---|---|---|---|---|---|---|
| Models with testlets | |||||||
| Hierarchical three-factor with testlets | 180 | 56 | 68 | 0.94 | 0.94 | 0.96 | 0.05 |
| Models without testlets | |||||||
| One-factor | 1497 | 170 | 1157 | 0.69 | 0.68 | 0.71 | 0.10 |
| Two-factor traditional | 743 | 118 | 507 | 0.82 | 0.82 | 0.84 | 0.08 |
| Two-factor amended | 948 | 134 | 680 | 0.79 | 0.79 | 0.82 | 0.09 |
| Hierarchical three-factor | 277 | 62 | 153 | 0.91 | 0.91 | 0.93 | 0.06 |
| Hierarchical four-factor | 669 | 131 | 407 | 0.85 | 0.86 | 0.88 | 0.07 |
| Hierarchical two-factor, four-facet | 629 | 130 | 369 | 0.86 | 0.87 | 0.89 | 0.07 |
| Correlated four-factor | 623 | 129 | 365 | 0.86 | 0.87 | 0.89 | 0.07 |
| Two-factor, four-facet parcelled | 1 | 1 | –1 | 1.00 | 1.00 | 1.00 | 0.02 |
| Two-factor, four-facet ‘wrong 1 factor’ | 981 | 130 | 721 | 0.79 | 0.77 | 0.81 | 0.09 |
| Two-factor, four-facet parcelled ‘wrong 1 factor’ | 1 | 1 | –1 | 1.00 | 1.00 | 1.00 | 0.00 |
AIC, Akaike information criterion; NFI, normed fit index; NNFI, non-normed fit index; CFI, comparative fit index; RMSEA, root mean square error of approximation
1. Swapped items: PCL4 with PCL10; PCL15 with PCL16
We then fitted the full three-factor hierarchical model with testlets (Reference ByrneCooke & Michie, 2001). This model achieves a close fit with a CFI of 0.96 and an RSMEA of 0.05 (Table 1).
Examining the impact of testlets
We then fitted a three-factor model with the testlet level removed. Such a model has been advocated by others on the grounds of parsimony. Using the criteria presented above this model achieves a fair and acceptable fit. However, the model with testlets achieves superior fit; direct comparison indicated that its fit is significantly better (Δχ2(4, n=827) =456, P<0.001). These results indicate that testlets provide a more comprehensive account of the measurement model underpinning the PCL–R. Despite the clear superiority of the original three-factor model, in the remaining analysis we excluded testlets to provide a more rigorous test of the three-factor model of the PCL–R. We call this model without testlets the degraded three-factor model.
Examining the fit of the fourth criminality ‘factor’
We then tested the three unparcelled four-factor models described in the literature; the four-factor hierarchical model, the two-factor, four-facet hierarchical model and the four-factor correlated model. None of these models achieve conventionally acceptable levels of fit (Table 1). Their level of fit is poorer than the level of fit achieved by even the degraded three-factor model.
Exploring the impact of parcelling
Parcelling, or adding individual items together prior to model fitting, was used to achieve the fit indices presented for the four-factor models in the PCL–R manual (Reference Floyd and WidamanHare, 2003: Figs 7.1, 7.3, 7.4). A prerequisite to parcelling is to demonstrate unidimensionality for the items being parcelled (Bandalos, 2002; Reference Harpur, Hakstian and HareKim & Hagtvet, 2003; Reference Maccallum and AustinRogers & Schmitt, 2004). The presence of testlets in PCL–R data (Reference ByrneCooke & Michie, 2001) means that this assumption is not met; that is, multiple latent constructs are tapped by items that are parcelled within individual factors of the four-factor models.
To examine the effects of parcelling on our dataset, we first estimated the two-factor, four-facet hierarchical model. Fit statistics (Table 1) indicate that this does not provide an adequate fit. We then parcelled the items by adding them together within their respective factor. We tested the fit of this model and fit statistics (Table 1) reveal a very good fit, with a non-significant χ2 value, and a CFI of 1.0.
We next tested the potential of parcelling to mislead. To do so, we compared the fit of an incorrect model that did, and did not, involve parcelling. The incorrect model involved swapping two item pairs within the two-factor, four-facet model: ‘pathological lying’ with ‘poor behavioural controls’ and ‘irresponsibility’ with ‘failure to accept responsibility for own actions’. Therefore, in this incorrect model, 4 of the 18 items loaded on the wrong factors. We then parcelled these 4 items into the same wrong factors.
Not surprisingly, the fit statistics for the unparcelled model indicate that swapping items substantially degraded the model's fit (Table 1). Indeed, the fit statistics suggest that this is an incorrect model. In contrast, the fit statistics for the parcelled model indicate an extremely good fit with a non-significant χ2 value, a CFI of 1.00 and a RMSEA of 0.00. We concluded that parcelling is an inappropriate technique when the intent is to understand the interrelations among PCL–R items.
DISCUSSION
These analyses yield three broad conclusions. First, of the unparcelled models, the original three-factor model with testlets achieves the best fit. Second, in keeping with the methodological literature, parcelling can achieve excellent fit even when items are placed on the wrong factor: it is thus an inappropriate analytical approach for understanding the structure of the PCL–R. Nonsensical models of PCL–R psychopathy can masquerade as ‘excellent fits’ when items are parcelled. Third, the analyses provide no evidence that models that add a criminal behaviour factor to the three-factor model achieve satisfactory fit.
Appropriate methods for modelling PCL-R scores
On grounds of empirical results, and on the grounds of theory, we argue that a comprehensive evaluation of the measurement model underpinning the PCL–R requires the specification of three broad factors that are underpinned by more specific testlets. On empirical grounds, this three-facet hierarchical model with testlets achieves a close fit. Although the model is not under-identified, as there are more observations than free model parameters (Reference Hart, Cox and HareKline, 1998), the model is not ideal because there are not enough indicators per testlet. The model is, however, the best that can be achieved within the psychometric limitations posed by the PCL–R (e.g. limited item coverage, local dependency). Even when the model is degraded by removing the testlet level, the fit achieved is fair. On theoretical grounds, the three-facet hierarchical model with testlets describes the broad interpersonal, affective and behavioural features that have traditionally been linked to the clinical construct of psychopathy. In addition, this model describes more specific facets at the testlet level, including, for example, deceptive interpersonal style and behavioural instability.
Is criminal behaviour central to the construct of psychopathy?
Proponents of the four-factor model(s) embrace the three Cooke & Michie factors within their models. The point at dispute is the role of additional items that essentially enumerate antisocial acts. None of the non-parcelled PCL–R models that add these antisocial behaviour items achieves acceptable fit. This indicates that these models do not provide adequate measurement models for the PCL–R. This is true whether the models involve hierarchical factors or (the less demanding) correlated factors. In our view there is no compelling empirical evidence to support the conclusion that antisocial behaviour is a central feature of psychopathy.
In addition, there are good conceptual (logical, theoretical) reasons for considering antisocial behaviour to be causally downstream from psychopathic personality disorder (Reference Chen and ThissenCooke et al, 2004; Reference OdgersSkeem &Cooke, 2007). First, classical clinical descriptions of psychopathy do not give a central role to antisocial behaviour (Reference Neumann, Kosson, Salekin, Herve and YuilleSchneider, 1950; Reference Hare and NeumannKarpman, 1961; Arieti, 1963; Reference Bentler and WuCleckley, 1988). As Blackburn (Reference Arieti2005) noted ‘criminal behavior was not intrinsic to Cleckley's concept’ (p. 279). Indeed, Cleckley (Reference Bentler and Wu1988), referring to the propensity to be antisocial in general, and seriously criminal in particular, indicated that ‘such tendencies should be regarded as the exception rather than as the rule, perhaps, as a pathologic trait independent, to a considerable degree, of the other manifestations which we regard as fundamental’ (p. 262). The critical feature for Cleckley was not the occurrence of criminal behaviour in itself but rather the occurrence of criminal behaviour for which the motivation is obscure. Simple counts of criminal acts cannot address this subtlety.
Second, it is plausible that the characteristic traits of psychopathy have a functional link with antisocial behaviour. Individuals who are grandiose frequently have a strong sense of entitlement that permits them to steal from, rape and exploit others. Those who lack empathy and anxiety may fail to inhibit violent thoughts and urges. Impulsivity increases the likelihood that these individuals will carry out criminal acts without considering the consequences (Reference Chen and ThissenCooke et al, 2004; Reference OdgersSkeem & Cooke, 2007).
Third, specific socially deviant acts are qualitatively different from the pervasive and persistent personality traits that underpin the three factors within the PCL–R (Reference Andershed, Kerr and StattinBlackburn, 1988). As Lilienfeld (Reference Hill, Neumann and Rogers1994) noted it is important not to conflate ‘basic tendencies’ (traits) and ‘characteristic adaptations’ (specific acts).
Fourth, antisocial behaviour has been linked to a number of mental disorders (e.g. psychotic disorders, learning disability, substance misuse and other personality disorders). It is thus a non-specific indicator (Reference Andershed, Kerr and StattinBlackburn, 1988; Reference Raine, Lencz and BihrleSkeem & Mulvey, 2001). Theories of crime have implicated a multitude of factors in relation to antisocial behaviour (Reference Cooke, Michie, Hart and PatrickGottfredson &Hirschi, 1990).
We would argue that there are thus strong theoretical and empirical reasons for excluding measures of criminal and antisocial acts from attempts to measure the construct of psychopathy; not least because it represents significant construct drift (Reference ArietiBlackburn, 2005).
The importance of understanding the structure of a measure
Some commentators have argued that the three-factor model differs very little from the two-factor model and it is of little importance whether two-, three-, or four-factor models are used. For example, Jones, et al (Reference Hare2007) expect the three- and four-factor models to ‘perform alike’ because the ‘models are quite similar’. They opine that the decision to use either model will hinge on personal preference or ‘researchers’ underlying conceptualisation of psychopathy'. We disagree. Given that the set of symptoms being modelled is the same, the content of any derived structure will inevitably be similar. This does not mean that the underlying structures are the same. Obtaining greater understanding of the structural properties of a disorder can yield many advantages (Reference Skeem and CookeWatson et al, 1994).
First, it can serve as a starting point for the identification of fundamental psychological structures or processes. Structural research on IQ tests revealed distinct verbal and spatial factors; subsequent neuropsychological research indicated that these factors measured separate neural sub-systems (Reference Skeem and CookeWatson et al, 1994).
Second, understanding structure can inform theories of causation: are the distinct facets products of some common underlying tendency towards psychopathy or are they not true facets but merely a number of distinct constructs without a common cause?
Third, explication of the structure can improve investigations of construct validity. If items are not grouped into unidimensional constructs, their relation to other variables in the nomological net may not be readily apparent. Associations with cognate variables based on a broad measure of a construct effectively average the associations underpinned by distinct factors; it is not clear which part of the measure drives the association, with the average association frequently being weaker than that of the strongest factor.
Fourth, an appreciation of structure can improve scales; and can provide direction on where new variables should be added to improve construct representation or removed to reduce construct-irrelevant variance (Reference Hill, Neumann and RogersLilienfeld, 1994; Reference Cooke, Michie and HartFloyd & Widaman, 1995; Reference Jackson, Rogers and NeumannLittle et al, 2002). Construct under-representation occurs when a measure fails to capture key aspects of the latent construct: it has been argued elsewhere, for example, that the PCL–R fails to adequately assess problems of self, attachment and interpersonal style which are central to the construct of psychopathy (Reference Cooke and MichieCooke et al, 2006). Construct-irrelevant variance occurs when the measure captures aspects of latent constructs other than the target latent construct. It is our contention (Reference Chen and ThissenCooke et al, 2004; Reference OdgersSkeem & Cooke, 2007) that the inclusion of counts of criminal and other antisocial behaviour in the PCL–R represents construct-irrelevant variance.
Conclusion
The validation of a construct is never complete. Validation is important for reasons of theory and for reasons of practice. The field is in danger of falling into the trap of operationalism: conflating a fallible measure of psychopathy (PCL–R) with the construct of psychopathy. Psychopathy and criminal behaviour are distinct constructs. If we are to understand their relationships and, critically, whether they have a functional relationship, it is essential that these constructs are measured separately. This is particularly critical within the context of the DSPD project, where individuals are detained because of the assumption of a functional link between their personality disorder and the risk that they pose. Recently, we have endeavoured to develop a more comprehensive model of the construct of psychopathy. Using clinical informants and a trait-descriptive adjectival approach we have identified – after numerous iterations – a list of 33 symptoms that are grouped rationally into six domains of functioning (interpersonal – attachment;behavioural; cognitive; interpersonal – dominance; emotional; and self). This model is currently being subjected to empirical evaluation.
This study is not without limitations. First, we were not able to test the various models on the data from the PCL–R manual (Reference Floyd and WidamanHare, 2003). Second, we were unable to demonstrate the chief problem inherent in correlated (rather than hierarchical) PCL–R model; that any correlate, whether essential to psychopathy or not, will fit. In future research, we will determine whether adding a non-psychopathic factor (e.g. addiction) to core PCL–R factors yields adequate fit indices in correlated factor models and (appropriately) poor fit indices in hierarchical models. Third, the results focus only on adult males prisoners; the generalisability of the results to other groups, including female offenders, remains unclear (Reference Cooke, Michie and HartForouzan & Cooke, 2005).
Acknowledgements
D.C. received support from the Research and Development Directorate of the Greater Glasgow Primary Care NHS Trust. We thank Brian Rae for his continued support and Stephen Hart for his comments and suggestions for particular analytical strategies.











eLetters
No eLetters have been published for this article.