Many years ago the physicist, Niels Bohr, observed dryly, ‘Predicting is very difficult, especially about the future.’ What is true in the field of physics appears to be true in the field of forensic mental health. Predicting whether or not individual people will engage in violence is one of the most practically and ethically troublesome of all clinical responsibilities (Reference Grisso and AppelbaumGrisso & Applebaum, 1992; Reference SzmuklerSzmukler, 2001). Research indicates that predictions of violence made using unaided (i.e. informal, impressionistic or intuitive) judgement are seriously limited with respect to both inter-clinician agreement and accuracy. This has motivated the development of a number of psychological tests commonly referred to as actuarial risk assessment instruments (ARAIs).
The ARAIs conceptualise violence risk solely in terms of probability of future violence, ignoring other facets of risk, such as the possible nature, severity, imminence, duration or frequency of future violence (Hart, Reference Hart, Douglas, Webster and Hart2001, Reference Hart2003). They use fixed and explicit algorithms, developed on the basis of data from known groups of recidivistic and non-recidivistic violent offenders and patients, to estimate the specific probability or absolute likelihood that a person will engage in violence in the future. The ARAIs increasingly are being used to determine whether a person should be incapacitated to prevent future violence. For example, in England and Wales ARAIs may play a central role in evaluations by psychiatrists and psychologists to determine whether a person should be committed indefinitely as a dangerous person with severe personality disorder, as well as whether these people, once committed, are now ready for release into the community (Reference Maden and TyrerMaden & Tyrer, 2003; Reference TyrerTyrer, 2004). In the United States, they are used in sex offender civil commitment and even capital sentencing evaluations (Reference JanusJanus, 2000; Reference HartHart, 2003).
The ARAIs differ from most psychological tests. Rather than being descriptive or diagnostic in nature, they are predictive or prognostic, designed solely to forecast the future. Findings of ARAI tests typically are interpreted using inductive logic, which can be expressed in the form of a syllogism, as follows.
-
• Major premise In the samples used to construct Test X, 52% of people with scores in Category Y were known to have committed violence during the follow-up period.
-
Minor premise Jones has a score on Test X that falls in Category Y.
-
Conclusion Therefore, the risk that Jones will commit future violence is similar to the risk of people in Category Y.
Findings of ARAI tests could also be interpreted using deductive logic, but few people appear to make the strong or rigid assumptions required for such an interpretation – namely, that all people belong to one of several naturally occurring discrete classes or categories, each class having a different probability of future violence, and that ARAIs determine the class to which a person belongs.
Given the high stakes of violence risk assessment, including evaluations of severe and dangerous personality disorders, forensic mental health professionals have an ethical responsibility to familiarise themselves with the limitations of ARAIs (Reference HeilbrunHeilbrun, 1992). Perhaps the most critical limitation is the ‘margin of error’ in risk estimates made using test scores. Staying with the example above, the findings of Test X for Jones indicate that he falls in a category for which the estimated risk of violence was 52%. This sounds ominous. But how precise or credible is this prediction? How much faith or confidence should we have in the test findings?
There are two major types of error relevant in the case of violence predictions made using ARAIs. The first is group error. The construction samples for Test X were just that – samples drawn from a larger population. The findings from the samples are used to draw inferences about the population parameter (i.e. the true rate of violence for the entire population of people who have scores in Category Y). We need to know the margin of error – typically expressed as a 95% CI – for the estimated violence risk associated with Category Y in the original construction samples.
The second type of error is individual error. Moving the focus of analysis from groups to individuals changes the way in which risk is conceptualised. According to ARAIs, violence risk is defined as the probability of violence. When considering groups, probability is defined in frequentist terms as the proportion of people who will commit violence (i.e. the relative frequency of events in a reference class; see Reference Hájek, Hall, Machamer and SilbersteinHájek & Hall, 2002), and the margin of error is uncertainty regarding the proportion of people who will commit violence. However, these definitions do not make sense for individuals, who either will or will not commit violence. (For a discussion of this ‘problem of the single case’ see Reference Hájek, Hall, Machamer and SilbersteinHájek & Hall, 2002.) When considering individuals the margin of error is uncertainty regarding whether a given person will commit violence. According to this view, the margin of error or uncertainty for an individual prediction is not the same as– and indeed, logically, must be considerably greater than – that for groups. Suppose a public opinion survey of 500 eligible voters found that 54% expressed their intent to cast ballots for candidate Smith in an upcoming election. This information allows one to forecast with reasonable confidence that candidate Smith will be elected by another group – namely, the general electorate. However, this same information does not allow one to predict the behaviour of a randomly selected voter with great confidence. Even though, in the absence of other relevant information, the most rational prediction is that every single voter will cast a ballot for candidate Smith, these individual predictions frequently will be wrong. So, to return to the ARAI example above, we need to know the margin of error for predictions made using Test X that a given person, such as Jones, will commit violence.
It is simply impossible to make rational, reasonable and legally defensible decisions based on the results of tests or statistical models without understanding the errors inherent in those results for both groups and individuals (with respect to forensic mental health, see Reference HeilbrunHeilbrun, 1992; with respect to medicine more generally, see Reference Henderson and KeidingHenderson& Keiding, 2005). However, surprisingly, these issues are rarely discussed in journal articles about ARAIs or in ARAI test manuals (but for noteworthy exceptions, see Reference Monahan, Steadman and AppelbaumMonahan et al, 2005, Reference MossmanMossman, 2006). In this paper, we re-analyse data from the development samples of the most commonly used ARAIs to calculate the margins of error for group and individual estimates of violence risk.
METHOD
Measures
We estimated the precision of violence predictions for two ARAIs, both constructed using a criterion groups design in which multivariate statistics were used to select and weight test items to maximise the discrimination between known groups of recidivists and non-recidivists. The tests were selected because they are frequently used, researched and discussed in Europe and North America.
Violence Risk Appraisal Guide
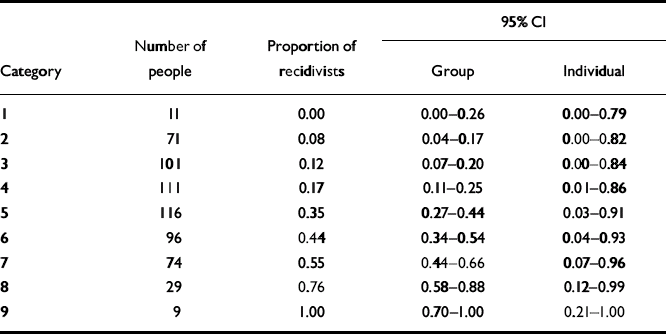
The Violence Risk Appraisal Guide (VRAG; Reference Quinsey, Harris and RiceQuinsey et al, 1998) is a 12-item test designed to assess risk for general violence over periods of 7–10 years. It was developed in a sample of patients released from a maximum-security forensic psychiatric hospital in Ontario, Canada. We evaluated the precision of risk estimates for violent recidivism over a 10-year follow-up period, following Quinsey et al (Reference Quinsey, Harris and Rice1998: Table A-1). The number of people and the corresponding proportion of recidivists for each of the nine score categories are presented in Table 1.
Table 1 Estimates of risk for groups and individuals with the Violence Risk Appraisal Guide
| 95% CI | |||||
|---|---|---|---|---|---|
| Category | Number of people | Proportion of recidivists | Group | Individual | |
| 1 | 11 | 0.00 | 0.00–0.26 | 0.00–0.79 | |
| 2 | 71 | 0.08 | 0.04–0.17 | 0.00–0.82 | |
| 3 | 101 | 0.12 | 0.07–0.20 | 0.00–0.84 | |
| 4 | 111 | 0.17 | 0.11–0.25 | 0.01–0.86 | |
| 5 | 116 | 0.35 | 0.27–0.44 | 0.03–0.91 | |
| 6 | 96 | 0.44 | 0.34–0.54 | 0.04–0.93 | |
| 7 | 74 | 0.55 | 0.44–0.66 | 0.07–0.96 | |
| 8 | 29 | 0.76 | 0.58–0.88 | 0.12–0.99 | |
| 9 | 9 | 1.00 | 0.70–1.00 | 0.21–1.00 | |
Static-99
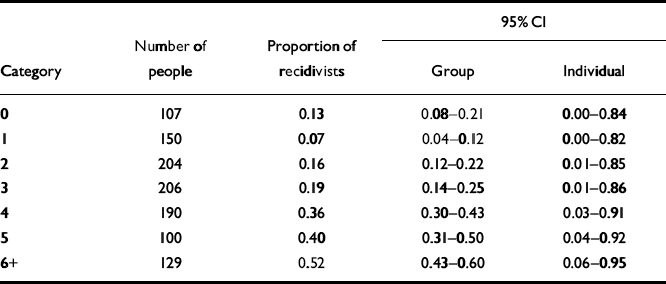
The Static-99 (Reference Hanson and ThorntonHanson & Thornton, 1999) is a 10-item test designed to assess risk for violence and sexual violence over periods of 5–15 years. It was developed from re-analyses of data from four diverse samples of offenders and forensic psychiatric patients released from institutions in Canada and the UK. We evaluated the precision of risk estimates for sexually violent recidivism over a 15-year follow-up period, following Hanson & Thornton (Reference Hanson and Thornton1999: Table 5). The number of people and the corresponding proportion of recidivists for each of the nine score categories are presented in Table 2.
Table 2 Estimates of risk for groups and individuals with the Static-99
| 95% CI | |||||
|---|---|---|---|---|---|
| Category | Number of people | Proportion of recidivists | Group | Individual | |
| 0 | 107 | 0.13 | 0.08–0.21 | 0.00–0.84 | |
| 1 | 150 | 0.07 | 0.04–0.12 | 0.00–0.82 | |
| 2 | 204 | 0.16 | 0.12–0.22 | 0.01–0.85 | |
| 3 | 206 | 0.19 | 0.14–0.25 | 0.01–0.86 | |
| 4 | 190 | 0.36 | 0.30–0.43 | 0.03–0.91 | |
| 5 | 100 | 0.40 | 0.31–0.50 | 0.04–0.92 | |
| 6+ | 129 | 0.52 | 0.43–0.60 | 0.06–0.95 | |
Statistical analyses
If one assumes that for a given ARAI score category group estimates of violence risk are binomial proportions, then it is possible to calculate the 95% CI using a method first outlined by Wilson (Reference Wilson1927). This method is relatively simple, carries a relatively low assumption burden and can be used without access to raw data. A recent review by Agresti & Coull (Reference Agresti and Coull1998) (see also Reference Brown, Cai and DasGuptaBrown et al, 2001) indicates that it is superior to some alternatives, such as the exact and Wald methods, because it not strongly influenced by extreme values with respect to sample size or the proportion of recidivists, and because it does not yield impossible values (e.g., negative lower limits).
According to Wilson's method, the upper limit (UL) and lower limit (LL) of the confidence interval are:
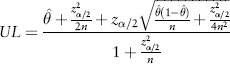
and
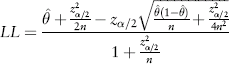
where n is the number of people in a given ARAI score category,
![]() \batchmode \documentclass[fleqn,10pt,legalpaper]{article} \usepackage{amssymb} \usepackage{amsfonts} \usepackage{amsmath} \pagestyle{empty} \begin{document} \({\hat{{\theta}}}\) \end{document}
is the proportion of recidivists in the score category and, for the purpose of constructing a 95% CI, z
α/2= 1.96.
\batchmode \documentclass[fleqn,10pt,legalpaper]{article} \usepackage{amssymb} \usepackage{amsfonts} \usepackage{amsmath} \pagestyle{empty} \begin{document} \({\hat{{\theta}}}\) \end{document}
is the proportion of recidivists in the score category and, for the purpose of constructing a 95% CI, z
α/2= 1.96.
We applied Wilson's method to the VRAG and Static-99. Based on published reports describing the construction of the tests, for each score category of the VRAG and Static-99 we calculated the precision of group estimates of violence risk with n equal to the number of people in the category and
![]() \batchmode \documentclass[fleqn,10pt,legalpaper]{article} \usepackage{amssymb} \usepackage{amsfonts} \usepackage{amsmath} \pagestyle{empty} \begin{document} \({\hat{{\theta}}}\) \end{document}
equal to the proportion of recidivists in the category. This is the standard and accepted application of Wilson's method. For group estimates of violence risk, the 95% CI is interpretable as follows: ‘Given a group of n people with ARAI scores in this particular category, we can state with 95% certainty that the proportion of recidivists will fall between the upper limit and lower limit.’
\batchmode \documentclass[fleqn,10pt,legalpaper]{article} \usepackage{amssymb} \usepackage{amsfonts} \usepackage{amsmath} \pagestyle{empty} \begin{document} \({\hat{{\theta}}}\) \end{document}
equal to the proportion of recidivists in the category. This is the standard and accepted application of Wilson's method. For group estimates of violence risk, the 95% CI is interpretable as follows: ‘Given a group of n people with ARAI scores in this particular category, we can state with 95% certainty that the proportion of recidivists will fall between the upper limit and lower limit.’
There are various ways to calculate the precision of individual estimates of violence risk. Perhaps the best methods come from logistic regression and event history analysis. With these methods, it is possible to model at the group level the occurrence of violence over a fixed time period (logistic regression analysis) or as a function of time (event history analysis), then to derive individual regression or survival scores and their respective margins of error. Unfortunately, the VRAG and Static-99 were not constructed using logistic regression or event history analysis, so it is impossible to evaluate the tests using these methods. Indeed, it appears to be impossible to calculate directly the precision of individual estimates of violence risk for any of the existing ARAIs using any standard statistical method, and so the only alternative is to use ad hoc procedures. The ad hoc procedure we selected was to apply Wilson's method to each score category of the VRAG and Static-99 with n equal to 1 and
![]() \batchmode \documentclass[fleqn,10pt,legalpaper]{article} \usepackage{amssymb} \usepackage{amsfonts} \usepackage{amsmath} \pagestyle{empty} \begin{document} \({\hat{{\theta}}}\) \end{document}
equal to the proportion of recidivists in the score category. For individual estimates of violence risk, we interpret the 95% CI as follows: ‘Given an individual with an ARAI score in this particular category, we can state with 95% certainty that the probability he will recidivate lies between the upper and lower limit.’ We piloted this application of Wilson's method in several prediction data-sets of our own and it yielded findings very similar to those obtained using logistic regression or event history analysis.
\batchmode \documentclass[fleqn,10pt,legalpaper]{article} \usepackage{amssymb} \usepackage{amsfonts} \usepackage{amsmath} \pagestyle{empty} \begin{document} \({\hat{{\theta}}}\) \end{document}
equal to the proportion of recidivists in the score category. For individual estimates of violence risk, we interpret the 95% CI as follows: ‘Given an individual with an ARAI score in this particular category, we can state with 95% certainty that the probability he will recidivate lies between the upper and lower limit.’ We piloted this application of Wilson's method in several prediction data-sets of our own and it yielded findings very similar to those obtained using logistic regression or event history analysis.
To illustrate our use of Wilson's method for determining group and individual margins of error, let us take an example. Suppose that Dealer, from an ordinary deck of cards, deals one to Player. If the card is a diamond, Player loses; but if the card is one of the other three suits, Player wins. After each deal, Dealer replaces the card and shuffles the deck. If Dealer and Player play 10 000 times, Player should be expected to win 75% of the time. Because the sample is so large, the margin of error for this group estimate is very small, with a 95% CI of 74–76% according to Wilson's method. Put simply, Player can be 95% certain that he will win between 74 and 76% of the time. However, as the number of plays decreases, the margin of error gets larger. If Dealer and Player play 1000 times, Player still should expect to win 75% of the time, but the 95% CI increases to 72–78%; if they play only 100 times, the 95% CI increases to 66–82%. Finally, suppose we want to estimate the individual margin of error. For a single deal, the estimated probability of a win is still 75% but the 95% CI is 12–99%. The simplest interpretation of this result is that Player cannot be highly confident that he will win – or lose – on a given deal.
RESULTS
Precision of group estimates
The 95% CI for group estimates for the score categories of the VRAG and Static-99 are shown in Tables 1 and 2 and Figs 1a and 2b. Looking first at the VRAG, the 95% CIs for score categories ranged from 13 to 30 percentage points in width, with a mean of about 20 percentage points. For the Static-99, the 95% CIs for score categories ranged from 8 to 19 percentage points in width, with a mean of about 13 percentage points. The somewhat smaller 95% CI for the Static-99 highlights the benefit of large sample sizes: increasing the number of people in a score category yields more precise group estimates.
Overlap among 95% CIs indicates that the group estimates for score categories did not differ significantly. Looking at the VRAG, the 95% CIs overlapped considerably and adjacent score categories almost always overlapped. This is most apparent in Fig. 1a. Categories 1–4 had overlapping 95% CIs. The 95% CIs for categories 5–7 overlapped with each other, but not with those of categories 1–4. The 95% CI for category 8 did not overlap with those of categories 1–6, but did overlap with that of category 7. The 95% CI for category 9 did not overlap with those of categories 1–7, but did overlap with that of category 8. These findings suggest that the VRAG score categories yield three reasonably distinct group estimates of risk: low (categories 1–4), moderate (categories 5–7) and high (categories 8–9).
Looking next at the Static-99, and in particular Fig. 2a, categories 0, 1, 2 and 3 had overlapping 95% CIs; categories 4, 5 and 6+ had 95% CIs that overlapped with each other but not with those of categories 0–3. Thus, the Static-99 yielded only two distinct group estimates of risk: low (categories 0–3) and high (categories 4–6+).
The greater number of distinct group estimates of risk on the VRAG highlights the importance of identifying extremely high risk or low risk groups: Even if score categories contain many people, unless the proportions of recidivists in various score categories differ substantially, their confidence intervals will overlap.
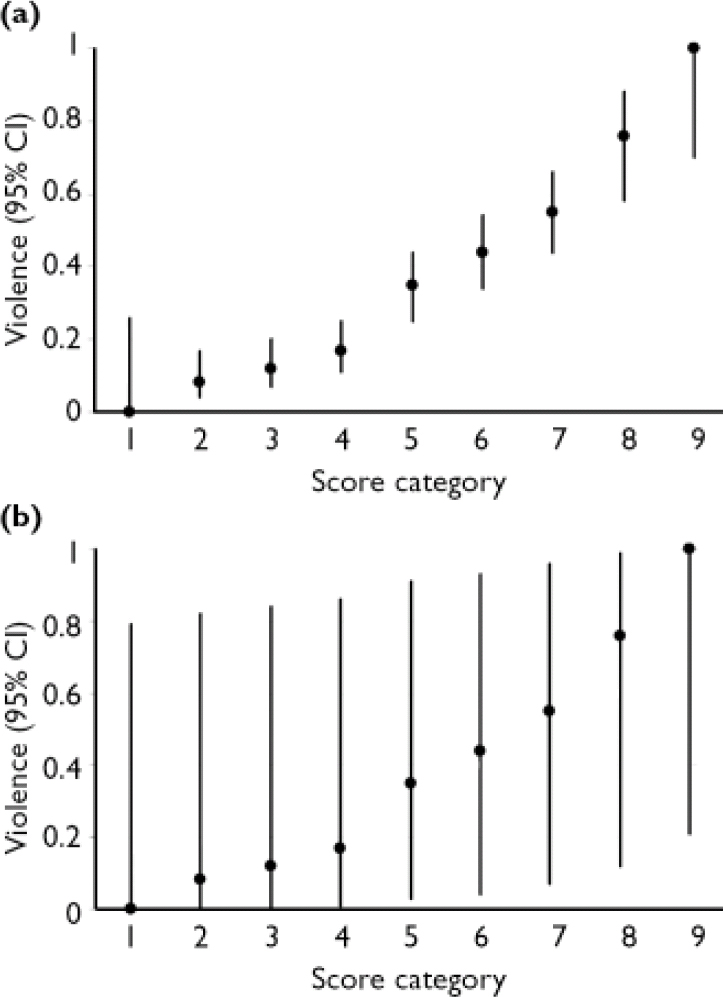
Fig. 1 Risk estimates (95% CI) for group (a) and individual (b) violence with the Violence Risk Appraisal Guide.
Precision of individual estimates
The 95% CIs for individual estimates of violence risk for the score categories of the VRAG and Static-99 are presented in Tables 1 and 2, and in Figs. 1b and 2b. For the VRAG, the 95% CIs for score categories ranged from 79 to 89 percentage points in width, with a mean of about 85 percentage points. For the Static-99, the 95% CIs for score categories ranged from 82 to 89 percentage points in width, with a mean of about 86 percentage points. The 95% CIs for score categories within each test overlapped almost completely, indicating that their risk estimates did not differ significantly. On neither test was there a score category that did not overlap with all the others; any distinctiveness of risk estimates for score categories at the group level did not translate into distinct risk estimates at the individual level.
DISCUSSION
Our analyses indicated that two popular ARAIs used in risk assessment have poor precision. The margins of error for risk estimates made using the tests were substantial, even at the group level. At the individual level, the margins of error were so high as to render the test results virtually meaningless. Our findings are consistent with Bohr's conclusion that predicting the future is very difficult.
Our findings likely come as no surprise to many people. The difficulties of predicting the outcomes for groups versus individuals – whether in the context of games of chance or of violence risk assessments – are intuitively obvious. Take, for example, the following quotation from Sir Arthur Conan Doyle's novel, The Sign of the Four:
‘[W]hile the individual man is an insoluble puzzle, in the aggregate he becomes a mathematical certainty. You can, for example, never foretell what any one man will do, but you can say with precision what an average number will be up to. Individuals vary, but percentages remain constant.’
Limitations
The method we used to estimate margins of error was introduced in the 1920s and is still accepted as equal or superior to its alternatives. It is, however, not without limitations.
With respect to estimating the precision of group predictions, Wilson's method assumes that people with scores in the same ARAI score category are homogeneous. However, ARAIs of 10 or 12 items almost certainly exclude potentially important information about risk, such as information about dynamic factors (e.g. Hart, Reference Hart1998, Reference Hart, Douglas, Webster and Hart2001) – and this is acknowledged by most authors (see Reference Quinsey, Harris and RiceQuinsey et al, 1998; Reference Hanson and ThorntonHanson& Thornton, 1999; Reference Monahan, Steadman and AppelbaumMonahan et al, 2005). Also, Wilson's method assumes that people are classified into ARAI score categories with perfect reliability. However, what little information is available in the published literature concerning the inter-clinician agreement for ARAI scores suggests that they are not perfect. If either of these assumptions is violated, then Wilson's method is overly conservative, and the tests' margins of error for groups are either larger than reported here or may even be incalculable.
With respect to estimating the precision of individual predictions, we were forced to use Wilson's method in an ad hoc manner. We recognise that some readers may object to this application but our pilot testing suggested that Wilson's method yields findings very similar to those obtained using more sophisticated methods for estimating the error of individual predictions based on raw data, such as logistic regression or event history analysis, which also suggest that individual prediction errors are extremely large (e.g., Reference Henderson and KeidingHenderson & Keiding, 2005). The only apparent alternatives to this ad hoc approach are: (a) to acknowledge that it is impossible to estimate the margin of error for individual predictions made using existing ARAIs and (b) to construct and evaluate new ARAIs using procedures that permit the direct estimation of the margin of error for individual predictions.
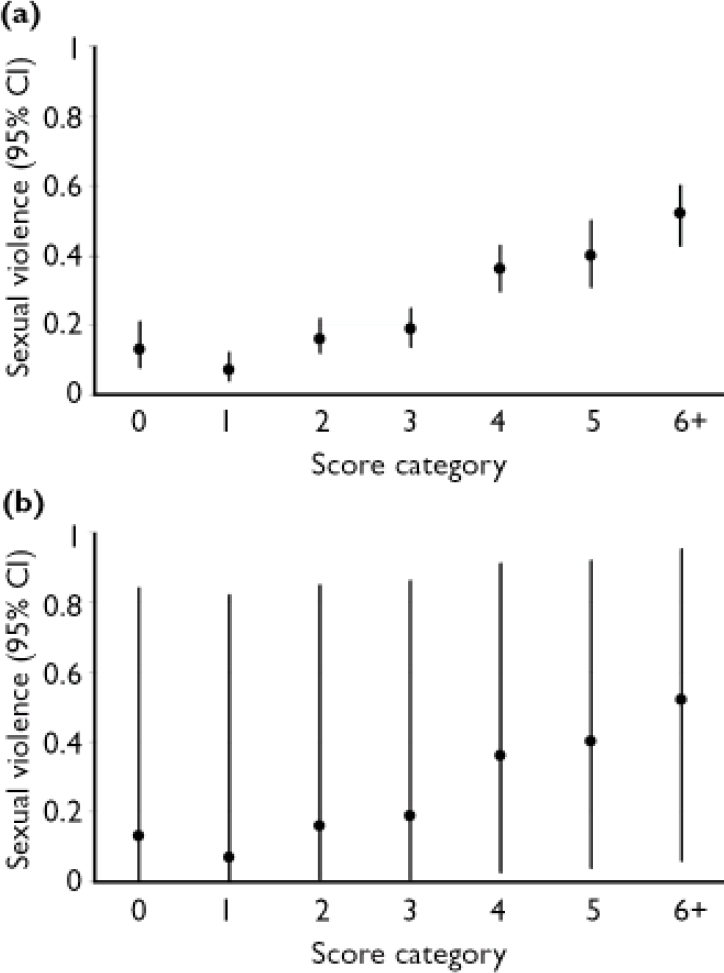
Fig. 2 Risk estimates for (95% CI) for group (a) and individual (b) violence with the Static-99).
Also with respect to estimating the precision of individual predictions, some readers may object to our application of Wilson's method because they interpret individual risk estimates as a person's propensity for future violence, not as a prediction of future violence. The problem is that this sort of ‘propensity’ bears no direct conceptual or statistical relation to an individual's actual behaviour (which, of course, has not yet occurred), making the entire concept a sort of metaphysical abstraction that is divorced from empirical reality (for clear and concise critiques of propensity approaches to probability, see Reference Hájek, Hall, Machamer and SilbersteinHájek& Hall, 2002 and Reference Hajek and ZaltaHájek, 2003). Thus anyone who relies on a propensity view of probability must also accept that it is impossible to use propensities to make specific predictions about the future violent behaviour of individuals with any reasonable degree of certainty.
Implications for forensic mental health evaluations
The potential implications of these findings for the practice of forensic mental health are profound. At best, they suggest that professionals should be extremely cautious when using ARAIs to estimate or draw inferences about an individual's risk for violence. This means, as Henderson & Keiding (Reference Henderson and Keiding2005) have recommended, ‘avoiding use of a single quantity to characterise a probability distribution, whether a point or categorical prediction, prognostic index, relative risk, or probability of surviving a given time’ (p. 705). At worst, they suggest that professionals should avoid using ARAIs altogether, as the predictive accuracy of these tests may be too low to support their use when making high-stakes decisions about individuals. Low predictive accuracy not only makes reliance on ARAIs ethically problematic, it also means that they may not meet legal standards for the admissibility of expert or scientific evidence. (For outlines of such criteria in the UK, see Reference Mackay, Colman, Thornton, Shepard, Heaton-Armstrong and WolchoverMackay et al, 1998 and Reference Zeedyk and RaittZeedyk & Raitt, 1998;for a discussion of criteria in the USA, see Reference FaigmanFaigman, 1995 and Reference Melton, Petrila and PoythressMelton et al, 1997.) Admissibility is also a problem if one concludes that margin of error for individual predictions is incalculable.
Another counter-argument presented to us is that ARAIs can be used appropriately as long as professional judgement or discretion is used to modify or override test-based decisions in the presence of relevant rare, case-specific or dynamic risk factors. According to Meehl (Reference Meehl1998), ‘This sounds amicable, tolerant, and even-handed, but it's actually stupid.’ The problem here is that it does not make sense to ‘fudge’ the results of a statistically derived estimate on the basis of personal preference; in addition, there is simply no empirical evidence that this improves the accuracy of predictions.
Finally, some professionals argue that it is appropriate to use ARAIs to make relative risk estimates concerning individuals (e.g. ‘Jones has a higher risk for violence than does Smith’). However, our findings indicate that the margin of error in group findings is substantial, leading to overlap among ARAI score categories. This means that it is perhaps difficult to state with a high degree of certainty that one individual's risk for future violence is higher than that of other individuals.
Test users should be very careful when using ARAIs to make sure that consumers of test findings (other mental health professionals, patients, courts, etc.) understand that it is, at least at present, impossible to make accurate predictions about individuals using these tests; this may help to minimise their potentially prejudicial impact on decision-making. Also, it may be wise to limit or avoid the use of ARAIs in situations where the cost of potential decision errors is high. An appropriate use of ARAIs may be for making administrative decisions regarding the frequency or intensity of risk management strategies recommended for a given individual (e.g. number of office visits, priority for admission into treatment groups). In such low-stakes circumstances, it may be reasonable to overlook numerous prediction errors at the individual level and focus on aggregate benefits at the group level.
Implications for the development and evaluation of ARAIs
Our findings also have implications for the development of ARAIs. First, they highlight the importance of large sample sizes. It is necessary to include many people in each ARAI score category, so that group estimates are reasonably precise. Typically, group sizes of ⩾500 are used in social science research (e.g. public opinion surveys); in biomedical research on mortality rates or in the insurance industry, group sizes are in the range of several thousand to tens or even hundreds of thousands. Second, our findings highlight the importance of identifying ARAI score categories with extreme estimates of violence risk. An example of ‘extreme’ estimates would be⩽10% v. 50% v. ⩾90%. Extreme group estimates may have non-overlapping 95% CIs. Only when both these conditions hold true can ARAIs yield potentially useful individual-level risk estimates. (Alternatively, test developers may wish to avoid altogether the concept of ‘groups’ and use statistical procedures that focus on individual predictions, such as logistic regression and event history methods. Of course, large sample sizes are no less important if this is the case.)
Our findings also suggest that people who develop and evaluate ARAIs should consider the potential benefits of conceptualising violence risk from a subjectivist perspective, focusing how evaluators do or should form beliefs about an individual's risk for future violence, especially in the light of uncertain information and decision errors with varying costs (e.g. Reference Hajek and ZaltaHájek, 2003). Although changing the discourse from frequentist to subjectivist will not make predictions of the future any more accurate, it may provide ways of researching and communicating about the problem that are more intuitively understandable to mental health professionals and legal decision-makers alike (for an example, see Reference MossmanMossman, 2006).
We conclude by advising readers that we have addressed only the rather limited issue of the margins of error of group- and individual-level risk estimates using ARAIs. We did not address other critical issues in construction and forensic use of ARAIs (e.g. Hart, Reference Hart, Douglas, Webster and Hart2001, Reference Hart2003; Reference LitwackLitwack, 2001): the questionable representativeness of their construction samples; the absence of calibration or cross-validation research on risk estimates, especially by independent researchers; problems with their legal relevance, owing to a failure to consider the presence of mental disorder and the presence of a causal nexus between mental disorder and violence risk; and their potential prejudicial impact on triers of fact.
Acknowledgements
We thank John Monahan, Douglas Mossman and David Thornton for their patient, lengthy and helpful critiques of earlier versions of this manuscript. D.J.C. received support from the Research and Development Directorate of the Greater Glasgow Primary Care National Health Service Trust while carrying out these analyses.









eLetters
No eLetters have been published for this article.